本文是关于经典聚类算法K-Means的代码实现。
一、实验目标
数据说明:目标是对 cluster.dat 里的数据进行聚类分析。其中,cluster.dat 包含了若干二维输入数据(但不包含其输出)。
使用 K-means 模型进行聚类,尝试使用不同的类别个数 K,并分析聚类结果。
按照 8:2 的比例随机将数据划分为训练集和测试集,至少尝试 3 个不同的 K 值,并画出不同 K 下的聚类结果,及不同模型在训练集和测试集上的损失。对结果进行讨论,发现能解释数据的最好的 K值。
二、实验环境
- 语言:Python 3.7(Anaconda3)
- IDE:PyCharm 2020.1.1 (Professional Edition)
- Packages:
- numpy:1.18.1
- matplotlib:3.1.3
三、算法原理
聚类是一种典型无监督学习,K-means算法是聚类的经典算法。目标是将原始数据集划分为k个簇,最小化损失函数(目标函数)是:
$$
SSE=\sum_{n=1}^{N}\sum_{k=1}^{K}r_{nk}dist(x_n-\mu_k)
$$
- $\mu_k$表示簇$C_k$的中心点(或其他能代表$C_k$的点)。
- $x_n$被划分到簇$C_k$则$r_{nk}=1$,否则$r_{nk}=0$。
- 目标是找到簇的中心点$\mu_k$及簇的划分$r_{nk}$使得目标函数SSE最小。
要解决上述问题就需要遍历所有可能的簇划分,显然这是不合适的。K-means算法使用了贪心策略求一个近似解,具体步骤如下:
- 将全部数据随机分为k类,计算每类的重心作为初始点。
- 计算所有数据点与各个簇中心之间的距离,将数据点划到与它距离最近的簇中。
- 根据簇中已有的样本点,重新计算簇中心(一般使用重心)。
- 重复2、3,直到数据点的簇划分不在变化或者达到了规定的最大迭代次数。
这是k-means算法的基本步骤,但是,这个算法有个很严重的问题,就是在将数据点划到与它距离最近的簇后,由于初始簇心选择不当,可能产生空簇,导致计算簇中心无法进行(簇的size=0,除数为0),我的解决方法是在计算簇心时,如果簇的size=0就先忽略,后面单独处理。计算完非空簇心后,依次选取与自己簇中心最远、次远……的点(因为距离自己的簇心越远,这个点分到该簇的概率越低)作为空簇的簇心,直到没有空簇,即所有的簇都有簇心,然后继续算法。
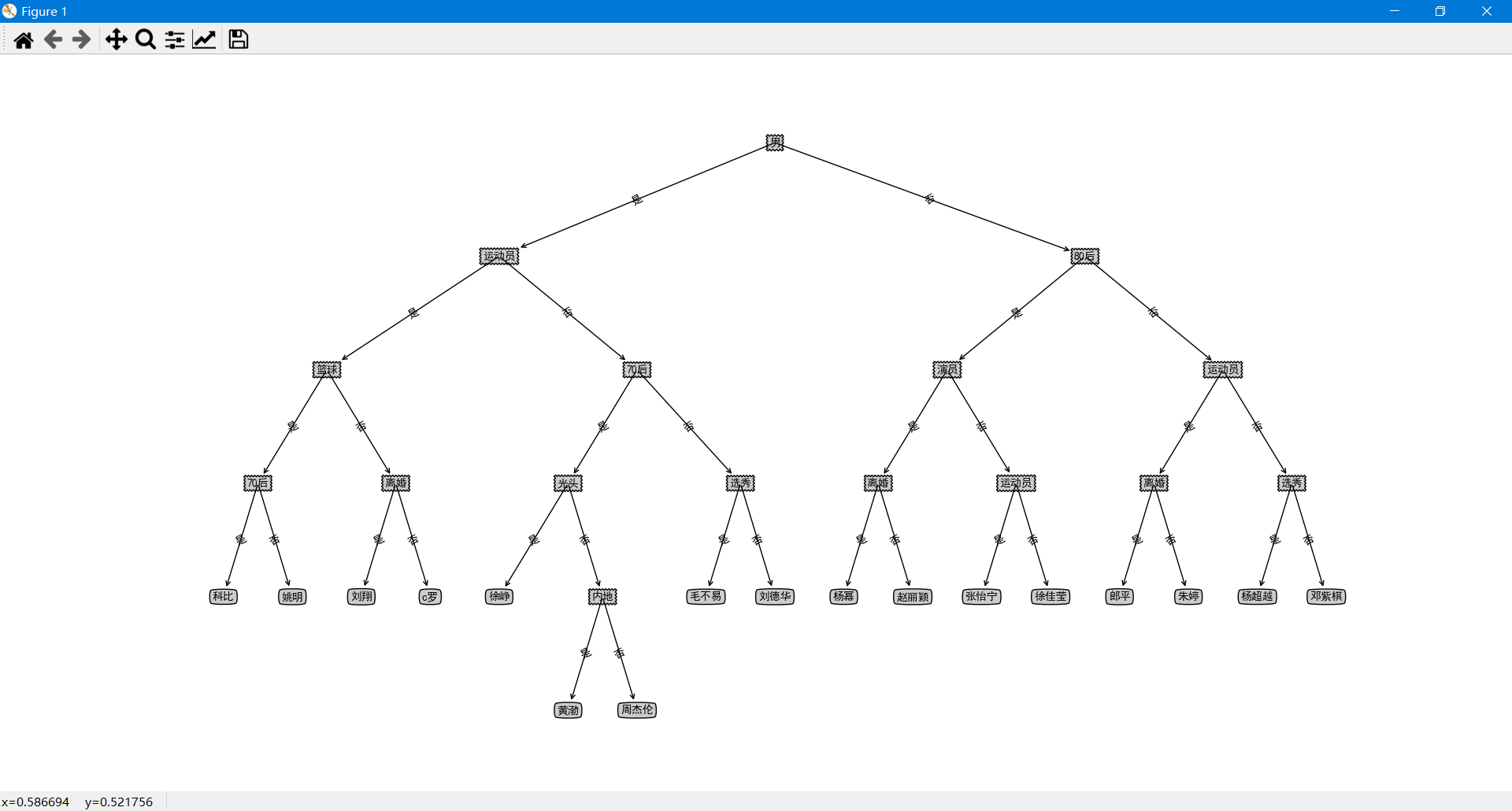
四、算法流程图
这只是算法函数(algorithm)和其他一些部分的流程图,不是整个程序的流程图,整个程序要更复杂。

五、实验结果及分析
输入k的范围是[2,10],测试集所占比例为0.2,最大迭代次数为20。
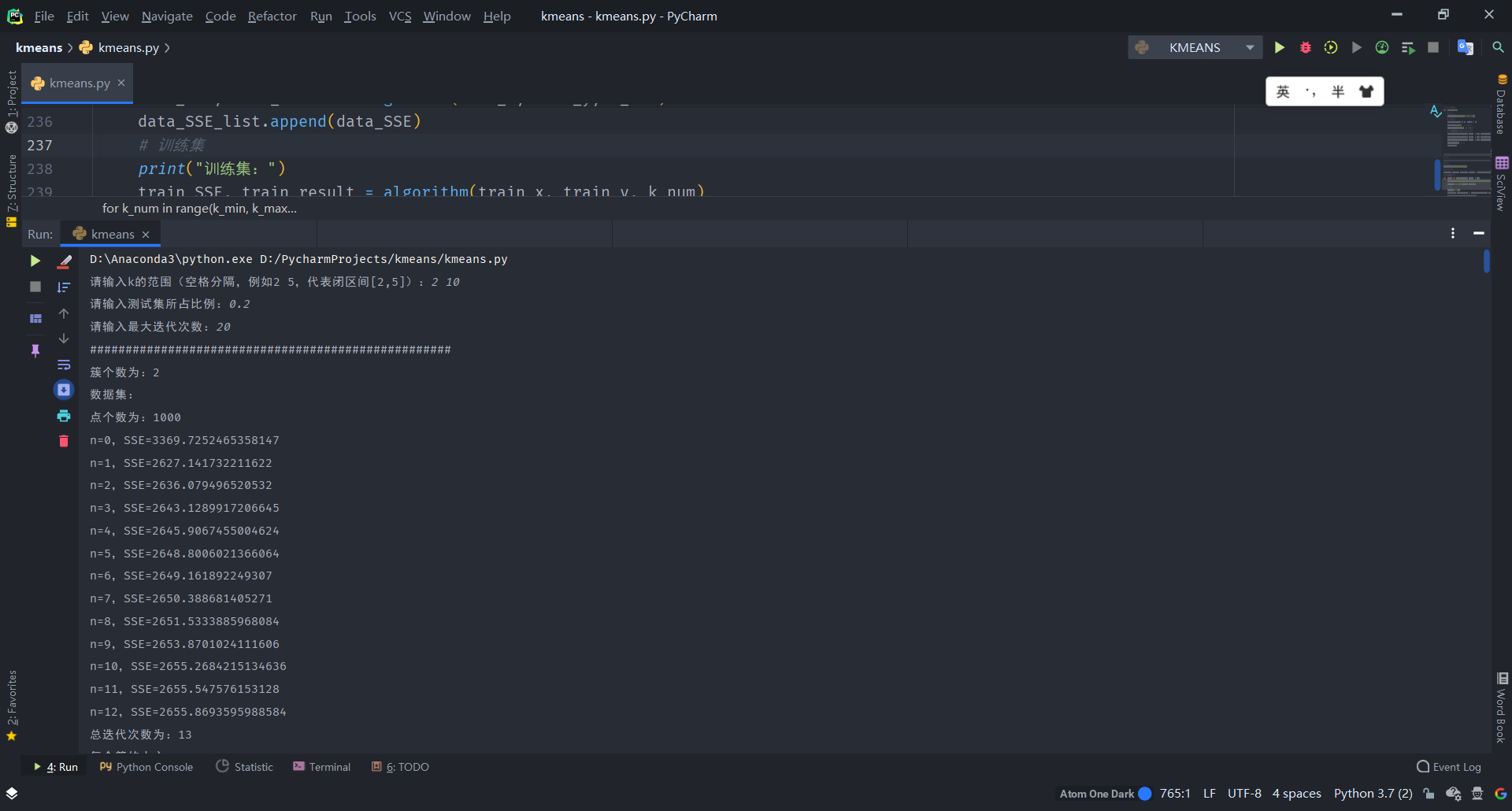
聚类结果
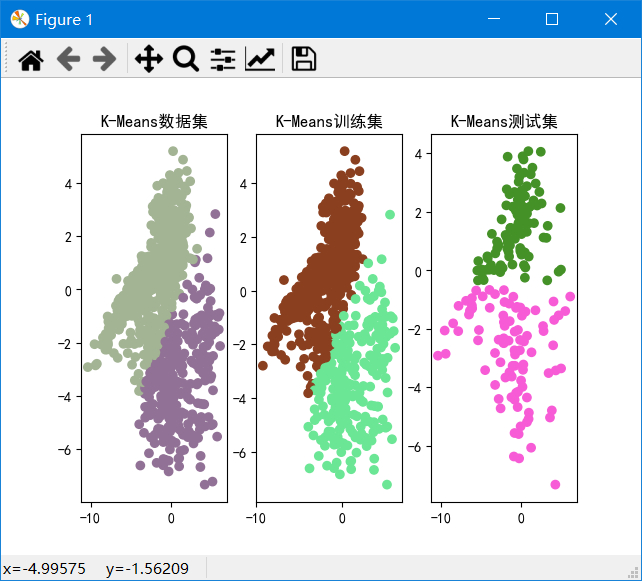
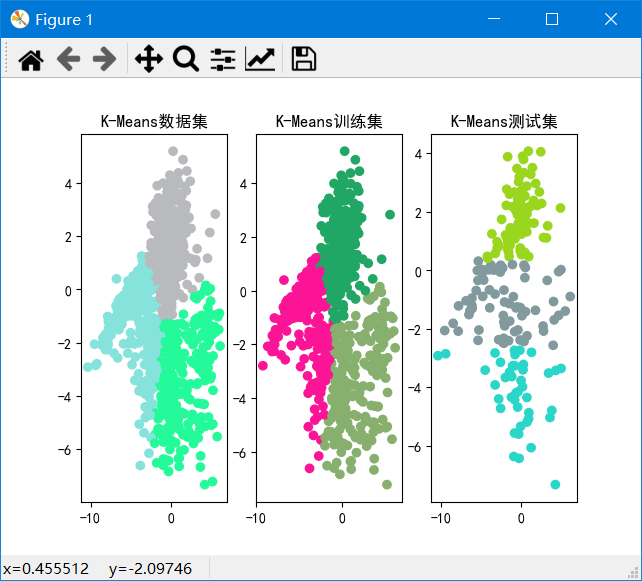
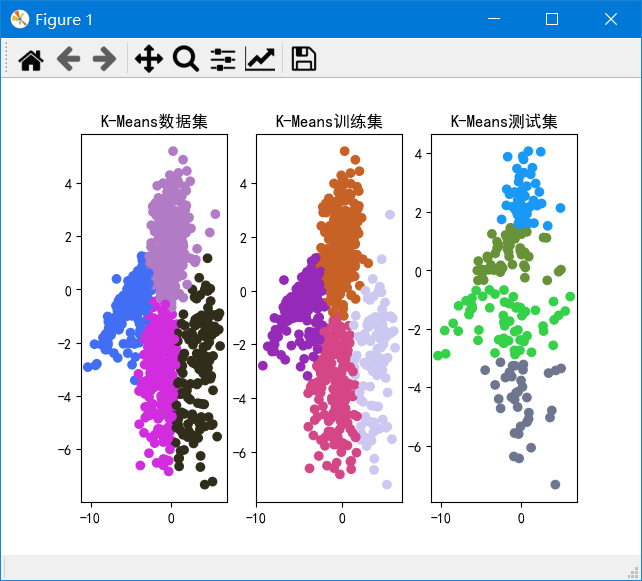
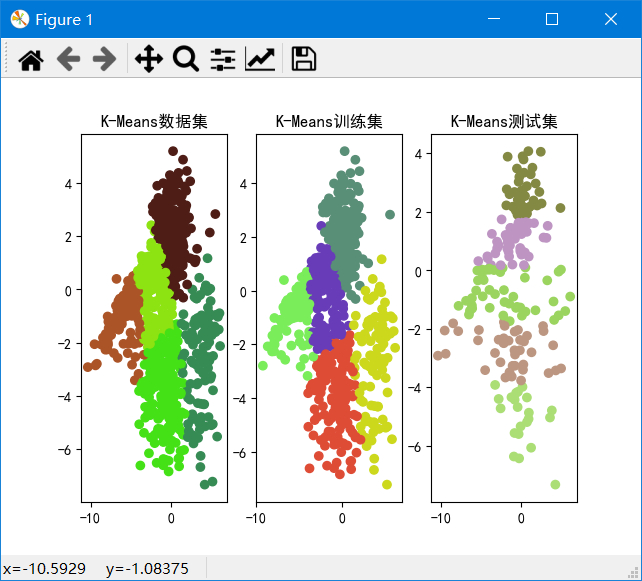
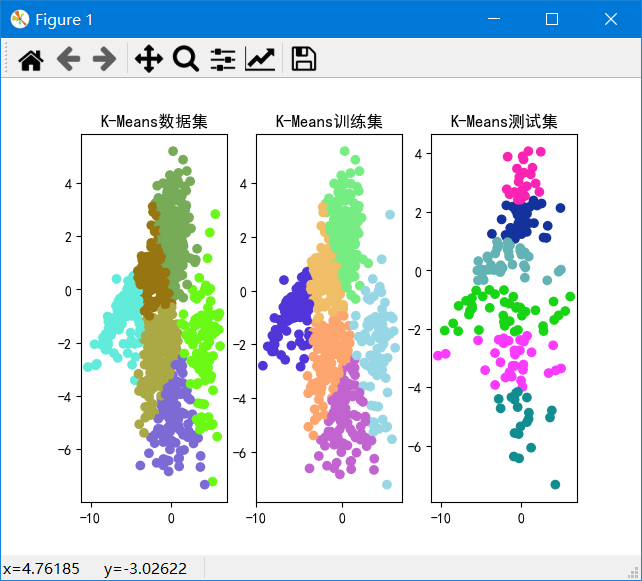
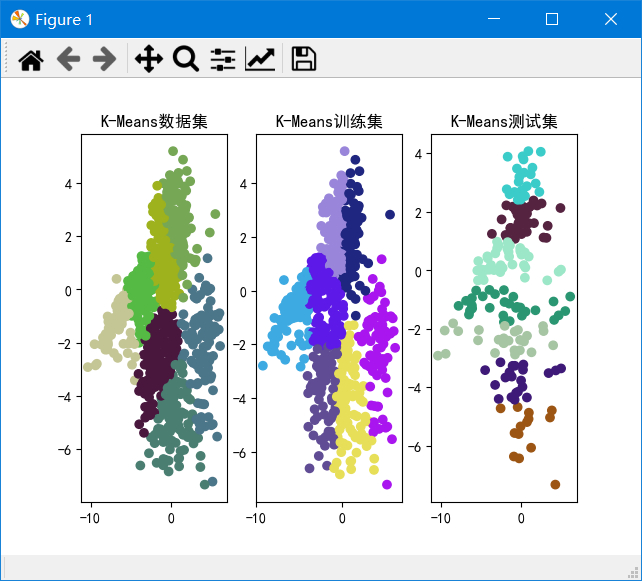
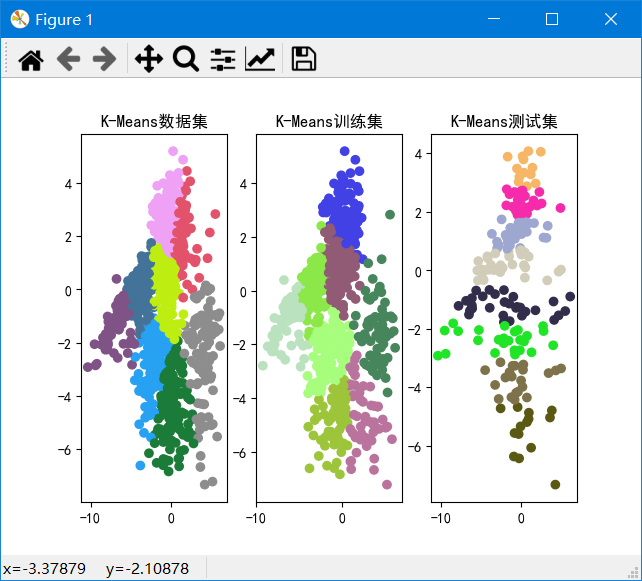
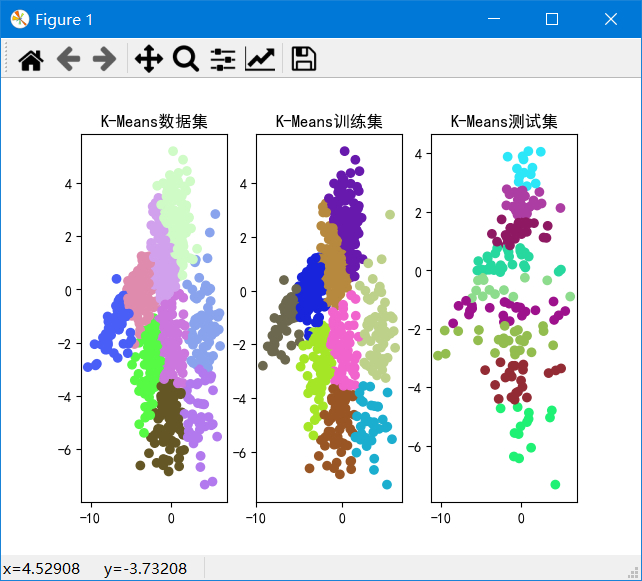
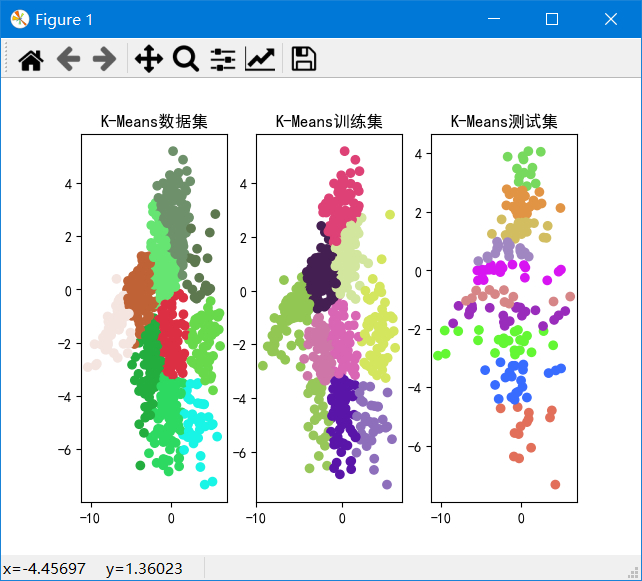
k从2~10的数据集、训练集和测试集的SSE如图:
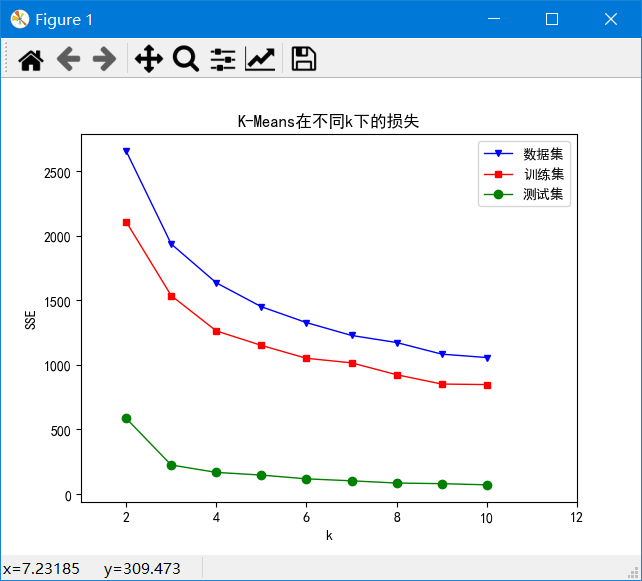
可以发现k=2~4时SSE下降较快,k=4~10时下降较慢,由于我们的目标是使SSE减小,因此由图可以得出k=4为解释数据较好的k。并且在k=2时,重复实验甚至会出现完全不同的聚类结果,说明k=2太小。在k>=6之后,SSE基本不下降,说明k再加大没有多大意义。
六、项目地址
本项目的源码、可执行程序均已经存放于我的Github,欢迎下载查看:
七、附录
kmeans.py:
1、基本配置、全局参数
点击查看代码
1 | import random |
2、读入数据
点击查看代码
1 | ######################################################## |
3、算法计算
点击查看代码
1 | ######################################################## |
4、画图展示
点击查看代码
1 | ######################################################## |
5、开始运行
点击查看代码
1 | ######################################################## |