机器学习 实验 决策树

Sekiro
机器学习实验

发布于：2020年4月26日
次浏览

字数：4.8k字

时长：20分钟
0  

本文是关于20问读心游戏的决策树代码实现。

一、问题：

以20问读心游戏为例，以ID3算法（即信息增益算法）为基础，构造并绘制决策树，最后可以进行简单的测试游玩.

二、实验环境

  • 语言：Python 3.6（Anaconda3）
  • IDE：PyCharm 2020.1.1 (Professional Edition)
  • Packages：
    • python standard library
    • numpy：1.16.2
    • scipy：1.2.1
    • pandas：0.24.2
    • networkx：2.4
    • graphviz：0.13.2
    • matplotlib：3.2.1

三、实验结果

2020-05-24_112450 2020-05-24_112723

四、项目地址

本项目的源码、可执行程序均已经存放于我的Github，欢迎下载查看：

五、附录

数据集data_set.txt：

点击查看

男 运动员 70后 光头 80后 离婚 选秀 篮球 内地 演员
是 是 否 否 是 否 否 是 是 否 姚明
是 是 否 否 是 是 否 否 是 否 刘翔
是 是 是 是 否 否 否 是 否 否 科比
是 是 否 否 是 否 否 否 否 否 c罗
是 否 否 否 否 否 否 否 否 是 刘德华
是 否 否 否 否 否 是 否 是 否 毛不易
是 否 是 否 否 否 否 否 否 是 周杰伦
是 否 是 否 否 否 否 否 是 是 黄渤
是 否 是 是 否 否 否 否 是 是 徐峥
否 是 否 否 是 否 否 否 是 否 张怡宁
否 是 否 否 否 是 否 否 是 否 郎平
否 是 否 否 否 否 否 否 是 否 朱婷
否 否 否 否 否 否 是 否 是 是 杨超越
否 否 否 否 是 是 否 否 是 是 杨幂
否 否 否 否 否 否 否 否 否 否 邓紫棋
否 否 否 否 是 否 是 否 否 否 徐佳莹
否 否 否 否 是 否 否 否 是 是 赵丽颖

代码decision_tree.py：

1、全局配置

点击查看代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# -*- coding: utf-8 -*-

from math import log
import matplotlib.pyplot as plt

########################################################
# 基本配置
########################################################


# 显示中文标签
plt.rcParams['font.sans-serif'] = ['SimHei']
# 设置决策树样式
# boxstyle为文本框的类型，sawtooth是锯齿形，fc是边框线粗细
# arrowstyle是树的线为箭头样式
decision_node = dict(boxstyle="sawtooth", fc="0.8")
leaf_node = dict(boxstyle="round4", fc="0.8")
arrow = dict(arrowstyle="<-")

2、构造决策树

点击查看代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
########################################################
# 构造决策树
########################################################


# 读入并创建数据集
def create_data_set():
    data_set = []
    # 数据从文件获取
    # f = open(r'data_set.txt', encoding='UTF-8')
    # text = f.read().splitlines()
    # print("data_set.txt的内容为：")
    # for line in text:
    #     temp = line.split('\t')
    #     print(temp)
    #     data_set.append(temp)
    # 数据在程序中写死
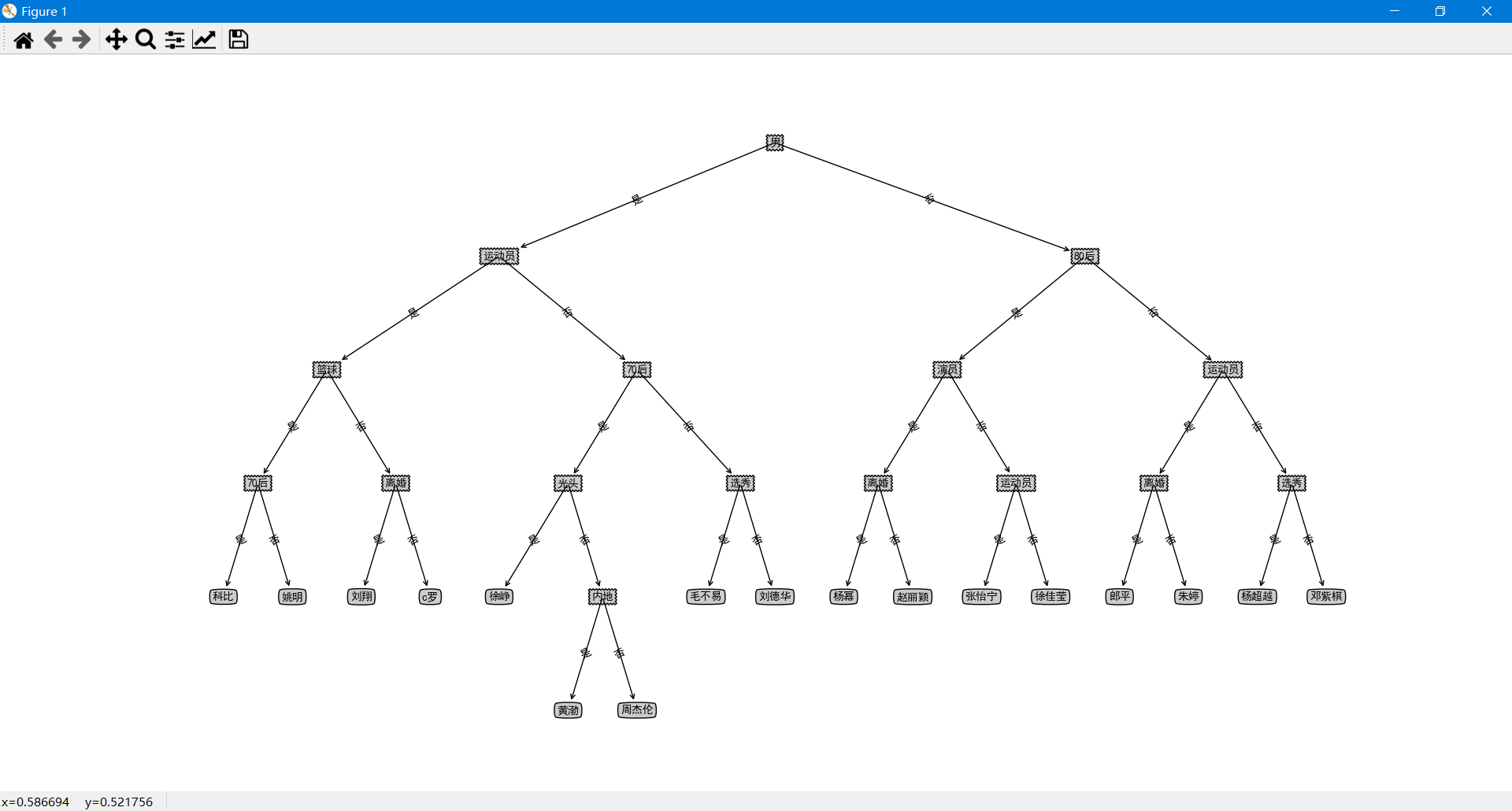
    data_set.append(["男", "运动员", "70后", "光头", "80后", "离婚", "选秀", "篮球", "内地", "演员"])
    data_set.append(["是", "是", "否", "否", "是", "否", "否", "是", "是", "否", "姚明"])
    data_set.append(["是", "是", "否", "否", "是", "是", "否", "否", "是", "否", "刘翔"])
    data_set.append(["是", "是", "是", "是", "否", "否", "否", "是", "否", "否", "科比"])
    data_set.append(["是", "是", "否", "否", "是", "否", "否", "否", "否", "否", "c罗"])
    data_set.append(["是", "否", "否", "否", "否", "否", "否", "否", "否", "是", "刘德华"])
    data_set.append(["是", "否", "否", "否", "否", "否", "是", "否", "是", "否", "毛不易"])
    data_set.append(["是", "否", "是", "否", "否", "否", "否", "否", "否", "是", "周杰伦"])
    data_set.append(["是", "否", "是", "否", "否", "否", "否", "否", "是", "是", "黄渤"])
    data_set.append(["是", "否", "是", "是", "否", "否", "否", "否", "是", "是", "徐峥"])
    data_set.append(["否", "是", "否", "否", "是", "否", "否", "否", "是", "否", "张怡宁"])
    data_set.append(["否", "是", "否", "否", "否", "是", "否", "否", "是", "否", "郎平"])
    data_set.append(["否", "是", "否", "否", "否", "否", "否", "否", "是", "否", "朱婷"])
    data_set.append(["否", "否", "否", "否", "否", "否", "是", "否", "是", "是", "杨超越"])
    data_set.append(["否", "否", "否", "否", "是", "是", "否", "否", "是", "是", "杨幂"])
    data_set.append(["否", "否", "否", "否", "否", "否", "否", "否", "否", "否", "邓紫棋"])
    data_set.append(["否", "否", "否", "否", "是", "否", "是", "否", "否", "否", "徐佳莹"])
    data_set.append(["否", "否", "否", "否", "是", "否", "否", "否", "是", "是", "赵丽颖"])
    attr = data_set[0]
    del (data_set[0])
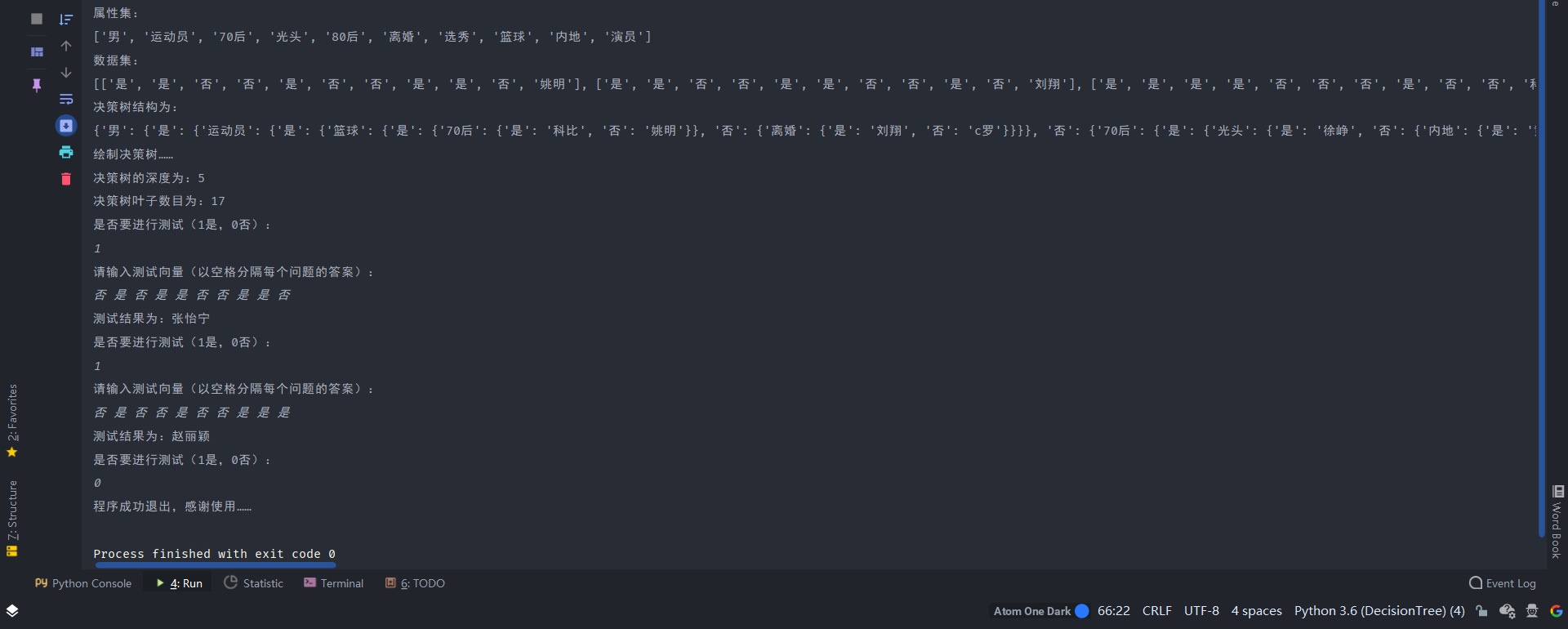
    print("属性集：")
    print(attr)
    print("数据集：")
    print(data_set)
    return data_set, attr


# 如果数据集中的axis列，值为value，那么取出这一行，且去掉这一列，加入子数据集中
def split_data_set(data_set, axis, value):
    sub_data_set = []
    for line in data_set:
        if line[axis] == value:
            # 去掉这一列
            # note: 用循环，较为麻烦
            # newline = []
            # for i in range(len(line)):
            #     if i != axis:
            #         newline.append(line[i])
            # sub_data_set.append(newline)
            # note: 易错点，如果直接newline = line，其实是newline和line指向同一个地址，会修改data_set中的值
            newline = line[:]
            del newline[axis]
            sub_data_set.append(newline)
    return sub_data_set


# 计算信息熵
def calc_info_ent(data_set):
    # 数据集样本条数n
    num = len(data_set)
    # 标签计数字典
    count = {}
    for i in data_set:
        # 获取样本最后一列的标签
        current_label = i[-1]
        # 如果当前标签不在计数字典里，则初始化
        if current_label not in count.keys():
            count[current_label] = 0
        count[current_label] += 1
    # 信息熵初始化
    info_ent = 0.0
    # 计算信息熵:sum(-P(X)log(P(x)))
    for key in count.keys():
        # 计算概率
        probability = float(count[key]) / num
        # -P(X)log(P(x))
        info_ent -= probability * log(probability, 2)
    return info_ent


# 选出信息增益最大的最优属性
def best_split(data_set):
    # 属性个数，data_set最后一列是标签，不是属性
    feature_num = len(data_set[0]) - 1
    # 初始信息熵,也就是根节点的信息熵
    base_ent = calc_info_ent(data_set)
    # 初始化
    best_info_gain = 0.0
    best_index = -1
    # axis为列号
    for axis in range(feature_num):
        # 获取每一列数据并去重
        row = []
        for line in data_set:
            row.append(line[axis])
        unique_row = set(row)
        new_ent = 0.0
        # value为列可能的取值，在20问读心游戏里为：是/否
        for value in unique_row:
            # 取出axis列的值为value的子数据集
            sub_data_set = split_data_set(data_set, axis, value)
            # 计算条件概率
            probability = float(len(sub_data_set)) / len(data_set)
            # 计算条件熵
            new_ent += probability * calc_info_ent(sub_data_set)
        # 计算信息增益
        info_gain = base_ent - new_ent
        if info_gain > best_info_gain:
            best_info_gain = info_gain
            best_index = axis
    return best_index


# 递归方式创建决策树
# data_set为当前数据集，attr为剩余的还未用过的属性集
def create_tree(data_set, attr):
    # 获取标签，data_set的最后一列
    # note: 因为递归，data_set会改变，每次要从新的data_set中获取
    true_labels = []
    for line in data_set:
        true_labels.append(line[-1])
    # 递归终止条件：标签全部相同（例如全是‘姚明’），或者只有一个标签，没必要再进行下去，直接返回这个标签
    if true_labels.count(true_labels[0]) == len(true_labels):
        return true_labels[0]
    # 递归终止条件：数据集中只有一个属性（只有一列，标签列，实际没有意义），没必要继续下去，直接返回列中相同值最多的标签
    if len(data_set[0]) == 1:
        return max(true_labels, key=true_labels.count)
    # 从当前数据集和剩余的属性集attr中获取最优属性(信息增益最大)的索引和属性名
    best_index = best_split(data_set)
    best_attr = attr[best_index]
    # 开始创建决策树
    # 初始化字典，创建根节点，第一个属性对应的也是一个字典
    root = {best_attr: {}}
    # 获取最优属性对应的列并去重
    best_row = []
    for line in data_set:
        best_row.append(line[best_index])
    unique_row = set(best_row)
    # value为列可能的取值，在20问读心游戏里为：是/否
    for value in unique_row:
        # 新建子属性集合，并且将用完的属性从属性集中删除
        # note: 最好是不要改变attr的内容，新建一个sub_attr拷贝attr，对sub_attr做删除操作
        sub_attr = attr[:]
        del sub_attr[best_index]
        # 递归构造决策树
        # note: root[best_attr]是一个字典
        #  根据当前best_attr属性的所有可能的取值value进行构造，在20问读心游戏里为：是/否
        #  也就是说构造出的决策树是二叉树
        root[best_attr][value] = create_tree(split_data_set(data_set, best_index, value), sub_attr)
    return root

3、绘制决策树

点击查看代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
########################################################
# 绘制决策树（ps: 为了让画出来的树更美观，借鉴学习了《机器学习实战》中的好思路）
########################################################


# 获取树的层数
def get_depth(decision_tree):
    max_depth = 0
    # 将决策树dict的key转化为list并获取根结点属性名称
    root_attr = list(decision_tree.keys())[0]
    # 根据根节点属性获取子树
    sub_tree = decision_tree[root_attr]
    # 对子树字典所有的key，也就是root_attr所有的取值（在20问读心游戏里为：是/否）遍历
    for key in sub_tree.keys():
        # 如果是字典对象，说明还未到叶子，继续递归
        if isinstance(sub_tree[key], dict):
            depth = get_depth(sub_tree[key]) + 1
        # 如果不是字典对象，说明已经到达叶子，停止递归
        else:
            depth = 1
        # 判断深度是否大于最大深度
        if depth > max_depth:
            max_depth = depth
    return max_depth


# 获取树的叶子节点个数，也就是标签数
def get_leaf_num(decision_tree):
    num = 0
    # 将决策树dict的key转化为list并获取根结点属性名称
    root_attr = list(decision_tree.keys())[0]
    # 根据根节点属性获取子树
    sub_tree = decision_tree[root_attr]
    # 对子树字典所有的key，也就是root_attr所有的取值（在20问读心游戏里为：是/否）遍历
    for key in sub_tree.keys():
        # 如果是字典对象，说明还未到叶子，继续递归
        if isinstance(sub_tree[key], dict):
            num += get_leaf_num(sub_tree[key])
        # 如果不是字典对象，说明已经到达叶子，停止递归
        else:
            num += 1
    return num


# 创建图对象，初始化，画图
def create_plot(decision_tree):
    # 定义一个背景为白色的画布，并把画布清空
    fig = plt.figure(1, facecolor='white')
    fig.clf()
    # ax_prop为图形的样式，没有坐标轴标签
    ax_prop = dict(xticks=[], yticks=[])
    # 使用subplot为定义了一个图，一行一列一个图，
    # frameon=False代表没有矩形边框
    # note: 在python里，[函数名称].[变量名]相当于是全局变量
    # ax1相当于是图对象，在其它函数中使用
    create_plot.ax1 = plt.subplot(111, frameon=False, **ax_prop)
    # total_width和total_depth分别代表初始决策树的叶子节点数目和深度，不改变
    plot_tree.total_width = float(get_leaf_num(decision_tree))
    plot_tree.total_depth = float(get_depth(decision_tree))
    # 图的大小是长0~1，宽0~1
    # note: x_offset实质是每个叶子的x坐标的位置
    #  第一片叶子的x为0.5/叶子数目，因此初始的x_offset设为-0.5/叶子数目
    #  每次将x_offset+(1/x_offset)，也就是第一个叶子不紧贴边框，有0.5/叶子数目的内边距
    #  例如绘制3个叶子，坐标应为1/3、2/3、3/3
    #  但这样整个图形会偏右，因此将初始的x_offset设为-0.5/3
    #  这样的话，每个叶子向左移了0.5/3，坐标变成了0.5/3、1.5/3、2.5/3，就刚好让图形在正中间了
    #  初始的y_offset显然为1，也就是最高点，每下降一层将y_offset-(1/深度)即可
    plot_tree.x_offset = -0.5 / plot_tree.total_width
    plot_tree.y_offset = 1.0
    # 初始根节点位置为图形的正中间最上方，即(0.5, 1.0)
    # 初始节点文本为空，等待获取
    plot_tree(decision_tree, (0.5, 1.0), '')
    plt.show()


# 递归画出决策树
# parent_pos为父节点位置，也就是当前决策树根节点的父节点位置
# arrow_text为父节点指来的箭头上的内容（在20问读心游戏里为：是/否）
def plot_tree(decision_tree, parent_pos, arrow_text):
    # 获取当前决策树叶子数目
    # note: leaf_num与plot_tree.total_depth不同，前者针对的是当前的决策树，后者是针对的原来的整个决策树
    leaf_num = get_leaf_num(decision_tree)
    # 将决策树dict的key转化为list并获取根结点属性名称
    root_attr = list(decision_tree.keys())[0]
    # root_pos为当前决策树的根节点的位置
    # note: 计算方法为
    #  拆分为三部分：
    #  1. plot_tree.x_offset：初始的x偏移，基准值
    #  2. float(numLeafs) / 2.0 / plotTree.totalW：
    #       float(numLeafs) * (1 / plotTree.totalW)为该决策树所包含的所有叶子所占的横坐标宽度
    #       / 2.0就是这个宽度的中间点
    #  3. 0.5 / plotTree.totalW：因为x_offset初始有-0.5/plotTree.totalW的偏移
    #       导致该节点并不是在区域中点，而是向左有个0.5/plotTree.totalW偏移
    #       因此+0.5 / plotTree.totalW，使其位于区域正中
    #  最终的公式经过合并就是下式：
    root_pos = (plot_tree.x_offset + (1.0 + float(leaf_num)) / 2.0 / plot_tree.total_width, plot_tree.y_offset)
    # 画出由当前子决策树父节点指来的箭头和箭头上的文本（在20问读心游戏里为：是/否）以及箭头指向的当前决策树的根节点
    plot_arrow_text(root_pos, parent_pos, arrow_text)
    # 节点类型为决策类型decision_node，不是叶子
    plot_node(root_pos, parent_pos, decision_node, root_attr)
    # 根据根节点属性获取子树
    sub_tree = decision_tree[root_attr]
    # note: 每下降一层，将y_offset减1.0 / plot_tree.total_depth
    plot_tree.y_offset = plot_tree.y_offset - 1.0 / plot_tree.total_depth
    # 对子树字典所有的key，也就是root_attr所有的取值（在20问读心游戏里为：是/否）遍历
    for key in sub_tree.keys():
        # 如果是字典对象，说明还未到叶子，继续递归
        if isinstance(sub_tree[key], dict):
            # note: 子决策树为sub_tree[key]
            #  子决策树的父节点为当前决策树的根节点
            #  当前决策树指向子决策树的箭头上的文本为key，因为key不是字符串，要进行类型转换
            plot_tree(sub_tree[key], root_pos, str(key))
        # 如果不是字典对象，说明已经到达叶子，停止递归
        else:
            # 每到一个叶子，就把x_offset加1.0 / plot_tree.total_width
            plot_tree.x_offset = plot_tree.x_offset + 1.0 / plot_tree.total_width
            # 画出叶子、箭头
            # (plot_tree.x_offset, plot_tree.y_offset)刚好是叶子的坐标
            # root_pos为当前决策树的根节点坐标
            # 节点类型为叶子类型leaf_node
            # 因为是叶子，sub_tree[key]为字符串类型，也就是标签
            plot_node((plot_tree.x_offset, plot_tree.y_offset), root_pos, leaf_node, sub_tree[key])
            # 画出箭头上的文本
            # 当前决策树指向叶子的箭头上的文本为key，因为key不是字符串，要进行类型转换
            plot_arrow_text((plot_tree.x_offset, plot_tree.y_offset), root_pos, str(key))
    # note: 易错点，每次递归结束需要将y_offset加1.0 / plot_tree.total_depth，回到上一层
    plot_tree.y_offset = plot_tree.y_offset + 1.0 / plot_tree.total_depth


# 画节点和指向节点的箭头的函数
# root_pos为子节点的位置，也就是箭头指向的位置
# parent_pos为父节点的位置，也就是箭头尾部所在的位置
# node_type为节点类型，两种：决策节点（decision_node）和叶节点（leaf_node）
# node_text为要显示的文本，也就是节点的内容，即属性的名称（例如：男、运动员……）
def plot_node(root_pos, parent_pos, node_type, node_text):
    # note: annotate用于在图形上给数据添加文本注解，支持带箭头的划线工具
    #  参数如下：
    #  s：注释文本的内容
    #  xy：被注释的坐标点，二维元组形如(x,y)
    #  xytext：注释文本的坐标点，也就是文本写的地方，也是二维元组，默认与xy相同
    #  xycoords：被注释点的坐标系属性，axes fraction是以子绘图区左下角为参考，单位是百分比
    #  textcoords：注释文本的坐标系属性，默认与xycoords属性值相同
    #  va="center"，ha="center"表示注释的坐标以注释框的正中心为准，而不是注释框的左下角(v代表垂直方向，h代表水平方向)
    #  bbox是注释框的风格和颜色深度，fc越小，注释框的颜色越深，支持输入一个字典
    #  arrowprops：箭头的样式，字典型数据，在画图的开头定义了
    create_plot.ax1.annotate(node_text, xy=parent_pos, xycoords='axes fraction',
                             xytext=root_pos, textcoords='axes fraction',
                             va="center", ha="center", bbox=node_type, arrowprops=arrow)


# 画箭头上文本的函数
# root_pos为子节点的位置，也就是箭头指向的位置
# parent_pos为父节点的位置，也就是箭头尾部所在的位置
# text为要显示的文本，也就是箭头上写的内容，即属性的取值（在20问读心游戏里为：是/否）
def plot_arrow_text(root_pos, parent_pos, arrow_text):
    # 文本的位置应该处于箭头中间，也就是文本坐标=箭头头坐标+（箭头尾坐标-箭头头坐标）/2，因为箭头是向下指的
    x_mid = root_pos[0] + (parent_pos[0] - root_pos[0]) / 2.0
    y_mid = root_pos[1] + (parent_pos[1] - root_pos[1]) / 2.0
    create_plot.ax1.text(x_mid, y_mid, arrow_text, va="center", ha="center", rotation=30)

4、测试函数

点击查看代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
########################################################
# 测试函数
########################################################


# 根据决策树decision_tree(决策树字典对象)和标签列表labels对输入的测试向量test进行分类，输出类别
# test为列表，样例：['是', '否', '否', '否', '否', '否', '否', '否', '否', '是']
# note: 与决策树建立一样，也是使用递归，从根节点查起，直到叶子
def classify(decision_tree, labels, test):
    # 将决策树dict的key转化为list并获取根结点属性名称
    # note: 易错点，如果不转化为list会产生错误：
    #  TypeError: 'dict_keys' object does not support indexing
    #  原因是python3改变了dict.keys，返回的是dict_keys对象，支持iterable
    #  但不支持indexable，我们可以将其明确的转化成list来解决
    root_attr = list(decision_tree.keys())[0]
    # 根据根节点属性获取子树
    # note: 子树也是一个字典对象，key为该属性的取值（在20问读心游戏里为：是/否）
    #  value也是一个字典对象，key为下一个属性，value为下一个属性对应的子树
    sub_tree = decision_tree[root_attr]
    # 根据根节点属性名称获取在标签列表中对应的索引，并根据索引获取测试向量test该属性对应的值（在20问读心游戏里为：是/否）
    value = test[labels.index(root_attr)]
    # 根据value的值（在20问读心游戏里为：是/否）获取决策树的子树字典
    tree_of_value = sub_tree[value]
    # 用isinstance判断得到的对象是不是字典对象
    # 如果是字典，就不是叶子，继续递归
    # 如果不是字典，就是叶子，停止递归，tree_of_value就是分类结果
    if isinstance(tree_of_value, dict):
        label = classify(tree_of_value, labels, test)
    else:
        label = tree_of_value
    return label

5、开始运行

点击查看代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
########################################################
# 开始运行
########################################################


# 读入并创建数据集和属性集
data_set, attr = create_data_set()
# 复制一份属性集attr用于递归，因为递归会将attr内容改变
attr_copy = attr.copy()
decision_tree = create_tree(data_set, attr_copy)
print("决策树结构为：")
print(decision_tree)
# 绘制决策树
print("绘制决策树……")
create_plot(decision_tree)
print("决策树的深度为：%d" % get_depth(decision_tree))
print("决策树叶子数目为：%d" % get_leaf_num(decision_tree))

6、测试游玩

点击查看代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
########################################################
# 测试
########################################################


print("是否要进行测试（1是，0否）：")
flag = int(input())
while flag == 1:
    print("请输入测试向量（以空格分隔每个问题的答案）：")
    test = input().split()
    result = classify(decision_tree, attr, test)
    print("测试结果为：%s" % result)
    print("是否要进行测试（1是，0否）：")
    flag = int(input())
print("程序成功退出，感谢使用……")
相关文章
机器学习 DNN 手写识别本文是关于经典深度神经网络DNN的应用手写识别的思路样例。机器学习 实验 K-Means聚类本文是关于经典聚类算法K-Means的代码实现。机器学习 实验 RNN 为baby起名字本文是关于经典RNN的应用为baby起名字的代码实现。Python 爬虫小Demo 学堂在线课程本文是关于Python中的Spider的小Demo，通过Python的scrapy爬取学堂在线课程的相关数据。现代交换原理 实验3 MPLS编程实验本文是关于交换原理实验三——MPLS编程实验报告记录。

本文为博主「Sekiro」的原创文章

内容遵循 署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0) 协议

本文永久链接是：https://666wxy666.github.io/2020/04/26/%E6%9C%BA%E5%99%A8%E5%AD%A6%E4%B9%A0-%E5%AE%9E%E9%AA%8C-%E5%86%B3%E7%AD%96%E6%A0%91/

更新于：2023年1月14日

Python

机器学习

决策树

评论




博客内容遵循 署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0) 协议

载入天数...载入时分秒...

Copyright © since 2020 Sekiro


PoweredHexo
HostedGitHub & Coding
CDNjsDelivr
ThemeVolantis