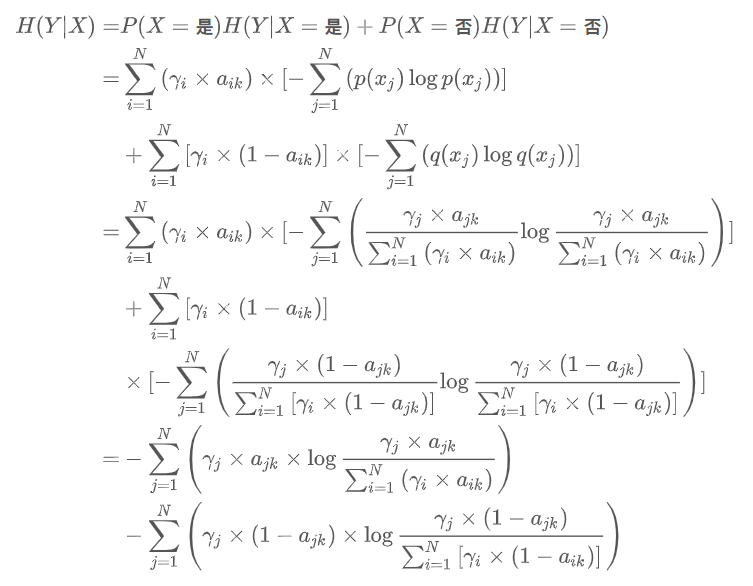机器学习 条件熵
本文是关于条件熵的知识拓展。
一、问题：
假定数据库有𝑁个人，第𝑛个人的先验概率$\gamma_n$，有𝐾个问题，假定第𝑛个人对第𝑘个问题答案为“是”的概率为$a_{nk}$，请给出给定第𝑘个问题条件下，数据集的条件熵的计算公式。
二、解析
原来的条件熵公式为：
$$
H(Y|X)=\sum_{x}{P(x)H(Y|X=x)}
$$
因为此题中X的取值只有两个即‘是’和‘否’，因此公式变为：
$$
H(Y|X)=P(X=是)H(Y|X=是)+P(X=否)H(Y|X=否)
$$
因此先计算对于第k个问题，X=‘是’的样本占总样本的概率P(X=是)和X=‘否’的样本占总样本的概率P(X=否)。
分子为对于第k个问题回答为‘是’的个数即：
$$
\sum^{N}_{i=1}{(N\times\gamma_i\times a_{ik})}
$$
分母为总数N，因此P(X=是)：
$$
P(X=是)=\frac{\sum^{N}_{i=1}{(N\times\gamma_i\times a_{ik}})}{N}
$$
$$
P(X=是)=\sum^{N}_{i=1}{(\gamma_i\times a_{ik})}
$$
同理，P(X=否)：
$$
P(X=否)=\frac{\sum^{N}_{i=1}{[N\times\gamma_i\times (1-a_{ik})}]}{N}
$$
$$
P(X=否)=\sum^{N}_{i=1}{[\gamma_i\times (1-a_{ik})]}
$$
然后在计算对于第k个问题，X=‘是’的数据集上Y的信息熵和X=‘否’的数据集上Y的信息熵，也就是：
$$
H(Y|X=是)=-\sum^{N}_{j=1}{(p(x_j)\log p(x_j))}
$$
$$
H(Y|X=否)=-\sum^{N}_{j=1}{(q(x_j)\log q(x_j))}
$$
因此要先计算对于第k个问题，X=‘是’的时候，对应每个人‘j’的概率$p(x_j)$。
分子为对于第k个问题，X=‘是’的时候，‘j’这个人的个数：
$$
N\times\gamma_j\times{a_{jk}}
$$
分母为对于第k个问题所有X=‘是’的个数，也就是上述的P(X=是)的分子：
$$
\sum^{N}_{i=1}{(N\times\gamma_i\times a_{ik})}
$$
或者写为：
$$
P(X=是)\times{N}
$$
因此$p(x_j)$：
$$
p(x_j)=\frac{N\times\gamma_j\times{a_{jk}}}{\sum^{N}_{i=1}{(N\times\gamma_i\times a_{ik}})}
$$
$$
p(x_j)=\frac{\gamma_j\times{a_{jk}}}{\sum^{N}_{i=1}{(\gamma_i\times a_{ik})}}
$$
同理X=‘否’的时候，对应每个人‘j’的概率$q(x_j)$：
$$
q(x_j)=\frac{N\times\gamma_j\times{(1-a_{jk})}}{\sum^{N}_{i=1}{[N\times\gamma_i\times (1-a_{jk})}]}
$$
$$
q(x_j)=\frac{\gamma_j\times{(1-a_{jk})}}{\sum^{N}_{i=1}{[\gamma_i\times (1-a_{jk})]}}
$$
综上所述，可以得出条件熵的最终公式为：
本文为博主「Sekiro」的原创文章
内容遵循 署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0) 协议
